高级加密标准 (AES) 已经成为很多应用(诸如嵌入式系统中的应用等)中日渐流行的密码规范。自从 2002 年美国国家标准技术研究所 (NIST) 将此规范选为标准规范以来,处理器、微控制器、FPGA和 SoC 应用的开发人员就开始利用 AES 来保护输入、输出及保存在系统中的数据。我们可在更高抽象层上非常高效地描述算法,就像用于传统软件开发中那样;但由于涉及到的操作,该算法在 FPGA中实现起来最为高效。开发人员甚至可在布线中“免费”获得一些操作。
本文引用地址:https://www.eepw.com.cn/article/201808/385496.htm基于这些原因,AES 是个绝佳的例子,即开发人员可利用 C 语言描述算法,然后在硬件中加速实现,从而受益于赛灵思 SDSoC ? 开发环境。本文中我们就是要这样做,首先熟悉一下 AES 算法,然后在赛灵思 Zynq?-7000 All Programmable SoC 的处理系统 (PS) 上实现 AES256(256 位秘钥长度)以建立软件性能基准,然后再在片上可编程逻辑 (PL)中进行加速。为了完全了解可获得的优势,我们将在 SDSoC 环境所支持的全部三个操作系统中执行这几个步骤,三个操作系统为:Linux、FreeRTOS 和裸机。

AES 属于对称块密码,可采用 128、192 和 256位不同的秘钥长度。秘钥长度决定加密或解密数据所需的处理步骤数。顾名思义,块密码算法采用的是数据块。AES 算法一次处理 16 字节的固定模块。因此,如果我们密码内容少于 16 字节,就必须将未使用的字节进行填充。
由于 AES 是对称密码,信息加密和解密都采用相同的做法和秘钥。相反,非对称算法(例如RSA)则使用不同秘钥进行数据加密和解密。
AES 算法中四个阶段中每个阶段都代表一个状态。四个 AES 阶段的组合称为一个循环。所需循环的数量取决于秘钥长度。
很简单,AES 状态起始于我们要加密的 16 个字节。每个新步骤都会对状态进行更新。处理状态之前,我们需要将输入字节串变为初始状态,即 4 x 4矩阵(图 1)。

图 1 — 16 字节的初始状态转换为 4 x 4 矩阵
现在,我们将最初的 16 个字节重新编排为 4 x4 矩阵形式的初始状态,便可研究每个步骤如何操纵它的输入状态。
轮密钥加(AddRoundKey) : 这是唯一使用加密秘钥的步骤。我们已经注意到,所需的加密算法循环的数量取决于秘钥长度(128、192 或 256 位)。必须对加密秘钥进行秘钥扩展,以确保在每个循环中不会重新使用秘钥中的字节。果然,对于不同的秘钥长度而言扩展秘钥长度并不相同。扩展秘钥长度为:
扩展秘钥长度(字节)= 16 *(循环 + 1)
这个步骤中的操作很简单。输入状态字节与扩展秘钥的 16 个字节进行异或运算。每个循环使用扩展秘钥的不同部分;循环 0 使用字节 0 至 15,循环1 使用字节 16 至 31,以此类推。对于每个循环,状态的字节 1 与扩展秘钥的最低有效字节进行异或运算,字节 2 与“最低有效字节+1”进行异或运算,以此类推。
字节替换 (SubBytes) : 该步骤利用字节替换将状态值用另一个值替换出去。替换盒中的值是预先设定的,而且输入位于输出位之间的关联较小。替换盒 (S-box) 是一个 16 x 16 矩阵。我们使用被替代字节的高四位和低四位作为替代表格中的索引。例如,使用图 2 中的 S-box 加密,如果第一个初始状态字节为 0 x 69,那么用替代值 0 x F9 代替。状态字节的高四位选择替代表格的行; 低四位选择列。注意在图 2 中,加密和解密使用不同的替换盒,而且盒中内容不同。

图 2 — AES S-box 内容
行位移变换 (ShiftRows) :该步骤对每行执行循环字节移位,以重新排列输入状态矩阵。 我们将每行右旋不同个因数(图 3)。第 1 行不变。将第 2 行移动 1 个字节,第 3 行移动 2 个字节,第 4 行移动3 个字节。解密时执行相同操作,但向左旋转而非向右。
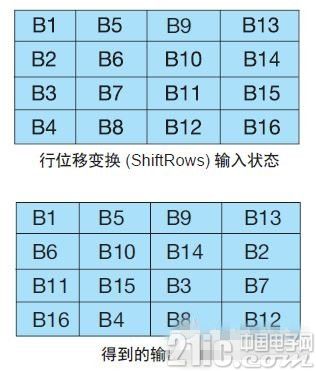
图 3 — 行位移变换 (ShiftRows) 操作
列混合变换 (MixColumns) :这是循环中最复杂的步骤,需要进行 16 次乘法和 12 次异或运算。逐列对输入状态矩阵进行此操作,将输入状态矩阵与固定矩阵相乘以获得新的状态列(图 4)。列中的每项与矩阵中的一行相乘。将每次乘法结果进行异或运算,以获得新的状态值。第一个要进行相乘运算的列和行在图 4 中加亮显示。
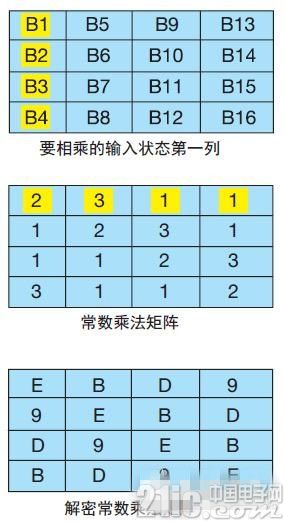
图 4 — 用于加密和解密的列混合变换 (MixColumns) 函数
以下是第一列的列混合变换(MixColumns) 方程:
B1’ = (B1 * 2) XOR (B2 * 3) XOR (B3 * 1) XOR (B4 * 1)
B2’ = (B1 * 1) XOR (B2 * 2) XOR (B3 * 3) XOR (B4 * 1)
B3’ = (B1 * 1) XOR (B2 * 1) XOR (B3 * 2) XOR (B4 * 3)
B4’ = (B1 * 3) XOR (B2 * 1) XOR (B3 * 1) XOR (B4 * 2)
然后,为输入状态中的下一个列采用相同乘法矩阵重复这个过程,直到处理完所有输入状态列。
既然我们已经理解了 AES 加密和解密算法所需的详细步骤,那么还需要知道一个循环中这些步骤的应用顺序以及我们是否必须为每个循环应用所有步骤。每个 AES 加密循环都包含全部四个步骤,并按照以下顺序:
1. 字节替换 (SubBytes) ;
2. 行位移变换 (ShiftRows);
3. 列混合变换 (MixColumns) (只针对循环 1 至N–1);
4. 轮密钥加 (AddRoundKey)( 使用扩展秘钥)。
当然,我们需要能够反转这个过程,将不可读的密文变回纯文本,让加密信息有用。为此,我们将步骤进行如下排序:
1. 反转行位移变换;
2. 反转字节替换;
3. 轮密钥加(使用扩展秘钥);
4. 反转列混合变换(只针对循环 1 至 N–1)。
执行第一轮加密之前,我们需要为加密和解密执行初始轮密钥加 (AddRoundKey) 操作。
可在更高抽象层上高效地描述 AES,就像在传统软件开发中那样,但在 FPGA 中实现起来最为高效。开发人员甚至可在布线中“免费”获得一些操作。我们看一下扩展秘钥必须使用的算法,以便提供足够的秘钥位,用以执行相应数量的轮密钥加(AddRoundKey) 步骤(图 5)。进行秘钥扩展时,16、24 或 32 字节的秘钥长度分别需要 44、52 或 60个循环。扩展秘钥的第一个字节等于初始秘钥。这意味着对于我们的 AES256 实例来说,扩展秘钥的最开始的 32 个字节就是秘钥本身。秘钥扩展操作在每次迭代中为扩展秘钥生成 32 个附加位。

图 5 — 秘钥扩展算法
扩展秘钥的第一个字节等于初始秘钥。这意味着对于我们的 AES256 实例来说,扩展秘钥的最开始的 32 个字节就是秘钥本身。以下是重要的扩展步骤:
RotateWord: 与行位移变换 (ShiftRows) 类似,这个步骤重新组织 32 位字,以使最高有效字节变为最低有效字节。
SubWord: 这个步骤使用的替换盒与加密时进行字节替换所使用的替换盒相同。
rcon: 该阶段对用户定义的值进行 2 次幂运算。
与列混合变换 (MixColumns) 阶段类似,rcon 也在有限域 (28) 中执行; 因此这个步骤普遍使用预先计算的查找表。
EK: 从扩展秘钥返回 4 个字节。
K: 与 EK 类似,从秘钥返回 4 个字节。
如何知道我们已经正确实现了加密和秘钥扩展算法? AES 的 NIST 规范包含多个有效实例,可用来检查我们自己的实现结果。
创建代码为了确保能够加速 Zynq SoC 的 PL 中 AES 代码的加密部分,我们必须一开始就要以这个目标来开发代码(见这里的编码规则)。要考虑的第一件事是算法的架构;我们需要正确对其进行分段。AES 很适合这种方案,因为我们可以为每个阶段编写函数,然后再根据需要调用。 我们还必须编写要在自身的文件中进行加速的函数。软件架构包括以下内容。
main.c: 该文件包含秘钥扩展算法、加密秘钥和纯文本输入,以及对 AES 加密函数的调用。
aes_enc.c: 该文件执行加密。我们将每个阶段编写为单独的函数,这样就能根据 AES 循环的需要进行调用。为确保程序设计对于处理器上执行的程序具有通用性,我们为混合步骤的乘法使用查找表。
aes_enc.h: 这个文件包含 aes_funcTIon 的定义以及用来确定大小的参数(例如 mk、nb 和 nr)。
sbox.h: 这个文件包含用于替换字节的替换盒、执行秘钥扩展的 rcon 函数的查找表以及用于列混合变换乘法的乘法查找表。
在这个结构中,我们可以选择 AES 加密函数( 图 6) 作为要进行加速的函数,只需右键点击该函数并选择“ Toggle HW/SW”即可。
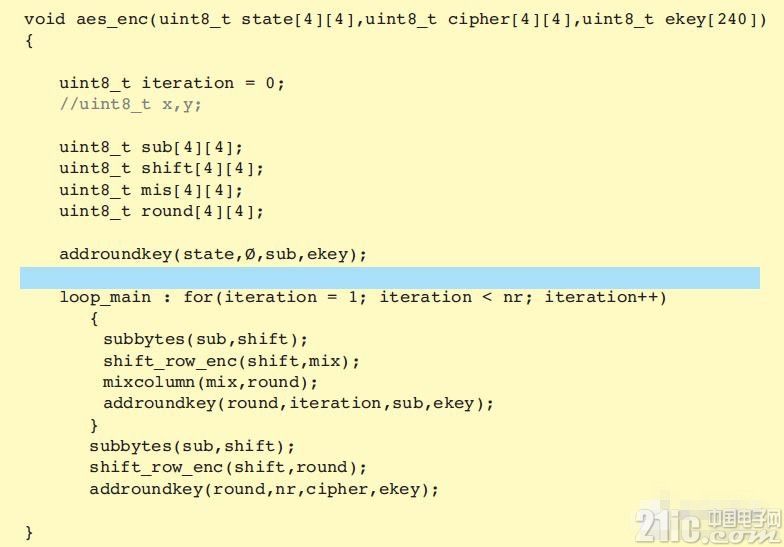
图 6 — 要加速的函数
为了能确定基准性能以及通过函数加速获得的保存结果,我们必须对函数的执行进行时间控制。为此,我们使用 sds_lib.h 中的sds_clock_counter。
编写源代码(在 github 提供)之后,在用 ZynqSoC 中的单个 ARM? Cortex ? -A9 处理器内核在软件中执行 AES 算法时,我记录了 36,662 个处理器周期。
为加速而进行的优化加速 AES 算法比前一个问题中的矩阵乘法算法还要稍稍复杂一些。这是因为 AES 算法的主循环包含互相依赖的阶段。
我加速 AES 算法时所采用的方法是:检查循环以找出可以展开的地方; 优化存储器带宽; 选择正确的数据移动时钟频率和硬件功能频率。
AES 加密函数的主循环包含用于执行每个 AES步骤的函数。AES 算法中的每个函数必须完整执行,并在下个函数运行之前计算出结果。这种互相依赖性需要我们将精力集中于作为独立函数的 AES步骤。这些步骤中存在足够多的优化潜力。
我们可将轮密钥加 (AddRoundKey) 、字节替换(SubBytes) 和列混合变换 (MixColumns) 步骤流水线化,以提高性能。在这些函数中,我们通过将编译指示放在第一个循环中来执行 HLS Pipeline 命令。我们应展开内部循环。这些函数中有几个函数从查找表(通常从 block RAM 构建)读取数据。我们需要增加存储器带宽,在本例中,我将编译指示参数指定为“完成”,这样可将存储器内容实现为分立寄存器而非BRAM。
在 Zynq SoC 上的 PS 与 PL 之间传输数据的能力对提升性能而言也非常重要。我所做的第一步是将数据移动时钟网络设定为最高时钟频率:200MHz。第二个方案是确保为 PS 与 PL 之间的数据传输使用直接存储器访问。为此,我必须将接口稍加修改,并使用 sds_alloc 函数按照 DMA 传输的要求确保数据在存储器中的连续性(图 7)。
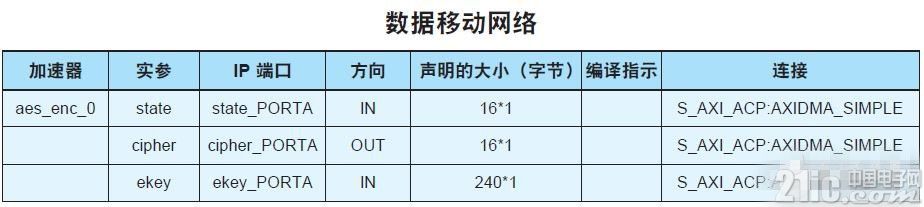
图 7 — PS 与 PL 之间的数据移动网络
第二个也是最后的优化步骤是将硬件功能的时钟速率设定在所支持的最高频率:166.67 MHz。
操作系统支持当我最终将所有内容放在一起并构建出这个实例时,经 PL 加速的 AES 代码在 Linux 上运行16,544 个处理器时钟周期; 当在单独在软件中运行
AES 代码时,只需要 45%(16,544/36,662) 的周期数量。这可将这个具有互相依赖关系且相当复杂的算法的执行时间缩短 55%。
当然,我们也可在 SDSoC 环境中选择 BareMetal或 FreeRTOS 操作系统。创建 BareMetal 和 FreeRTOS项目并重新使用代码能够在三种操作系统之间进行性能对比。对于给定项目而言,操作系统的选择取决于任务要求、性能预算以及响应时间。
图 8 给出了 Zynq SoC 的 PS 和 PL 中三种操作系统的性能( 图 8)。

图 8 — Zynq PS 和 PL 中的操作系统性能。FreeRTOS 和 BareMetal 提供类似的缩短效果。
不出意料,FreeRTOS 和 BareMetal 实现了类似的时间缩短效果,因为两种操作系统都比完整的 LinuxOS 简单得多。
正如我们的结果所示,利用 SDSoC 开发环境加速 AES 加密,能实现真正的性能提升,而且易于实现—— 无需深入的 FPGA 设计经验。