蒙特·卡罗方法是从赌场诞生的算法,如今已经走到了科技前沿。它是用随机的蛮力对抗精确逻辑的浪漫,也是用数量得到质量的神话。大道至简,回到最初的蒙特卡罗方法,教会我们保有最初做学问的本心,进一寸有一寸的欢喜。或许很多事情,都只是一万次的尝试而已。
今天的主题蒙特卡罗(Monte Carlo)大有来头。它是摩纳哥的一个地区,被称作“摩纳哥的钻石”。这里有赛车、有歌剧、有芭蕾……还有举世闻名的赌场,各种邦德电影,赌神系列,想想就让人血脉偾张。

为什么我们会提到这里的花花赌场?是因为从前有个老头,常常在摩纳哥的蒙特卡洛赌场输钱。他有个好侄子,是数学家斯塔尼斯拉夫·乌拉姆(Stanislaw Ulam),是不到20岁就以证明无穷集合重要定理而留名数学史的神童、极具原创力的几大科学领域的先驱、鲜为人知的“氢弹之父”。乌拉姆还有位要好的同事叫做冯·诺伊曼(John von Neumann),是著名的“计算机之父”、“博弈论之父”。20世纪40年代,科学家冯·诺伊曼、斯塔尼斯拉夫·乌拉姆、尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡罗方法。

该方法因乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输钱得名,而蒙特卡罗方法正是以概率为基础的方法。真正是,有的人去赌场,只是去赌钱,有的人去赌场,就发明了最好用的概率论算法。
实际上,蒙特卡洛是一种计算方法。简单来说,我们尝试收集大量随机样本,样本容量越大,概率上就越能接近我们所求的结果。譬如我们抛一万次硬币,那么几乎可以肯定,大致会得到一半正面、一半反面的结果。
我们来举个最常见的例子:π值的估算。
我们思考一下这个图型。假定正方形的边长是2,那么正方形的面积就是4。同时圆的直径是2,半径是1,所以圆的面积正好是π。
想象整个正方形区域是片沙漠,圆是一个湖泊。如果我们在空中随机跳伞,降落在湖里的几率应该是π/4。
现在我们派一万个虚拟的小人去“跳伞”。也就是说我们随机生成一万个正方形内的点,并且根据在不在圆内对他们进行分类。我们知道圆内的点与总数的比例应该大约是π:4。
我们随机生成的点越多,这个结果也就越准确。根据这个简单例子,大家对蒙特卡罗方法应该有一个大概的印象了。乍一听起来,好像十分没有技术含量,像是一个很原始,很直接的方法。但是对很多问题来说,这就是唯一解法。
我说了不算数,但是我一直很喜欢《三体》里描述蒙特卡罗方法的这一段话。很精确,甚至有种人道主义的浪漫。所谓大道至简,有时候解决最复杂的问题,只需要用到最简单的方法。
《三体》里的魏成是这样介绍蒙特卡罗算法的:
“那是一种计算不规则图形面积的计算机程序算法,具体做法是在软件中用大量的小球随机击打那块不规则图形……这种方法虽然简单,却展示了数学中的一种用随机的蛮力对抗精确逻辑的思想方法,一种用数量得到质量的计算思想。这就是我解决三体问题的策略。”
从估算π的值到三体问题,听起来好像天方夜谭一样。这就是蒙特卡罗方法的魅力所在。上至天文,下到地理,万物皆可蒙特卡罗。往近了说,你想积个分,这是蒙特卡罗的基本应用。往远了说,你跟AlphaGo下个棋,也会用到蒙特卡罗树。
拿定积分来说,我们知道定积分的值实际上是一个函数在某一段和x轴组成图形的面积,可以说是正中下怀。我们来考虑这样一个函数,
。我们想要求在0到1 之间, f(x) 的定积分,也就是
的值。我们知道所有的函数值都在0到1之间,也就是说我们要求的这个不规则图形一定在这个1比1的正方形里。大概长这样。
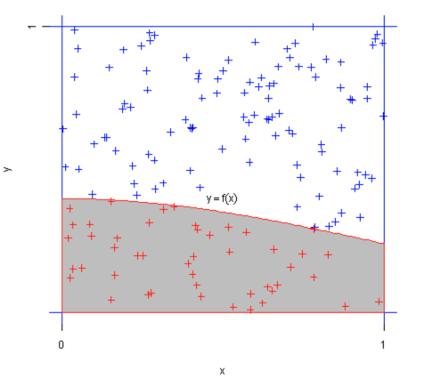
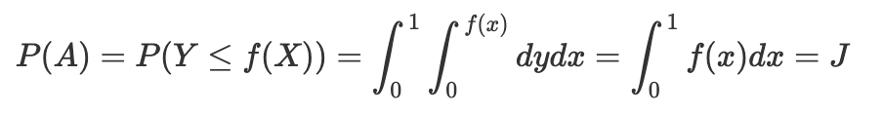

一个棋盘,每个位置下黑子或者白子,一共有成千上万种不同的变换。计算机要做的是计算这成千上万种变换,并且根据赢面最大的几种方法决定下一步要怎么走。在确定赢面最大的走法的时候,AlphaGo会根据以往的数据,来猜测对手会怎样走。根据对手的走法,AlphaGo会计算下一步怎样走胜率更大。蒙特卡罗树,就利用了各种各样的比率,确保我们只往胜率最大的情况进行推演,大量减少计算率。就可以抛弃很多无用的线路,不用暴力走到白头。为什么蒙特卡罗树在机器学习中十分有用?因为蒙特卡罗树在前期积累了很多随机的棋谱,是机器自己跟自己下棋,产生了很多很多路线,都储存在蒙特卡罗树里,这样就能够帮助机器筛选把好棋和臭棋区分开来,从而大量减少计算量。如果你想了解更多关于AlphaGo的算法。推荐大家看一看同名纪录片《Alpha Go》。
想必大家对蒙特到底是什么卡罗应该有个大体的印象了。这是从赌场诞生的算法,一路走到科技前沿。是用随机的蛮力对抗精确逻辑的浪漫,也是用数量得到质量的神话。大道至简,回到最初的蒙特卡罗方法,教会我们保有最初做学问的本心,进一寸有一寸的欢喜。或许很多事情,都只是一万次的尝试而已。
* 本文内容属罗博深数学及其母公司Expii, Inc所有,如需转载请联系罗博深数学团队,未经授权请勿转载。欢迎转发本文与全世界的朋友分享数学、教育的乐趣。
原标题:《有的人去赌场赌钱,他却发明了最好用的概率论算法》